The development of new combustion chambers requires the increasing use of numerical simulation. Simulation has to provide an accurate estimation of heat release rates, ignition delay times, pollutant formation, etc. The use of realistic kinetic models is essential for the estimation of these data. Detailed kinetic models are developed to provide accurate estimates over a wide range of pressure, temperature, and mixture composition. Depending on the complexity of the initial fuel, the detailed model can be composed of a few dozen species (H₂) to a few thousand (C₁₀H₂₂). However, the numerical solution of complex reactive systems involving detailed kinetic mechanisms is very challenging. In this context, a large number of numerical methods have emerged with the aim of simplifying combustion kinetic mechanisms, by limiting the number of species involved (which directly governs the number of species conservation equations to be solved) and/or by limiting the stiffness of the differential equations to be solved.

Development of a reduction tool (Brookesia)

A kinetic mechanism reduction and optimization software tool has been developed to adapt the mechanisms for the simulation of reactive flows in combustion chambers in complex configurations. This tool, developed in native Python language, is based on reduction algorithms found in the literature (Sensitivity analysis (SA), Directed Relation Graph (*), Directed Relation Graph with Error Propagation (**), Sensitivity Analysis coupled with Relation Graph with Error Propagation (SARGEP)) and then applies, if necessary, a subsequent optimization (Genetic Algorithm (***) or Particle Swarm Optimization) of the reduced mechanism to compensate for the errors arising from the loss of information inherent in the reduction procedure.

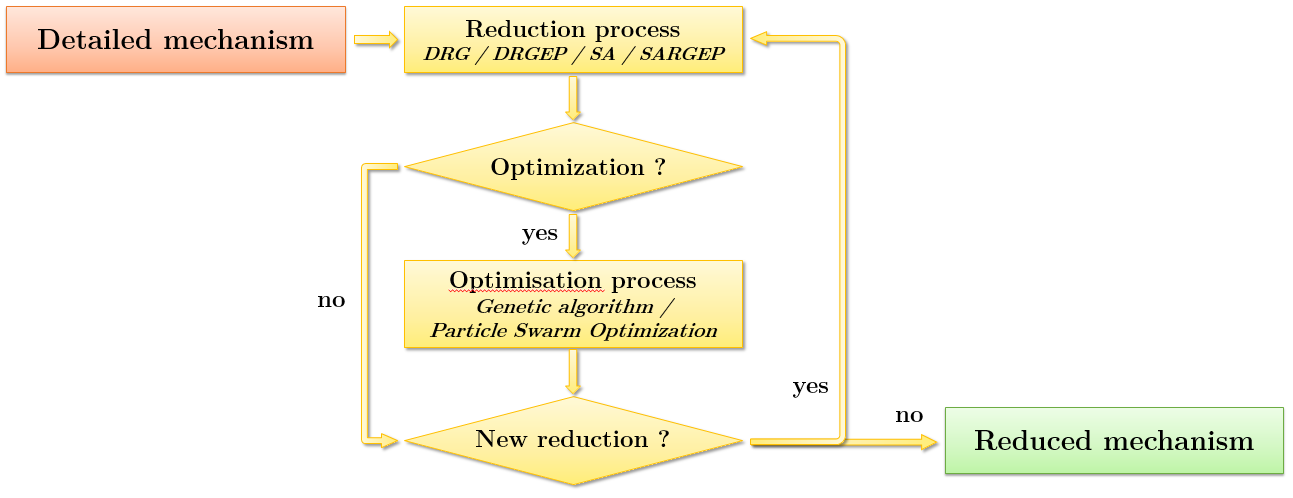
The overall algorithm of the code is shown in figure 1. As mentioned earlier, several reduction methods can be used in succession with or without optimization.

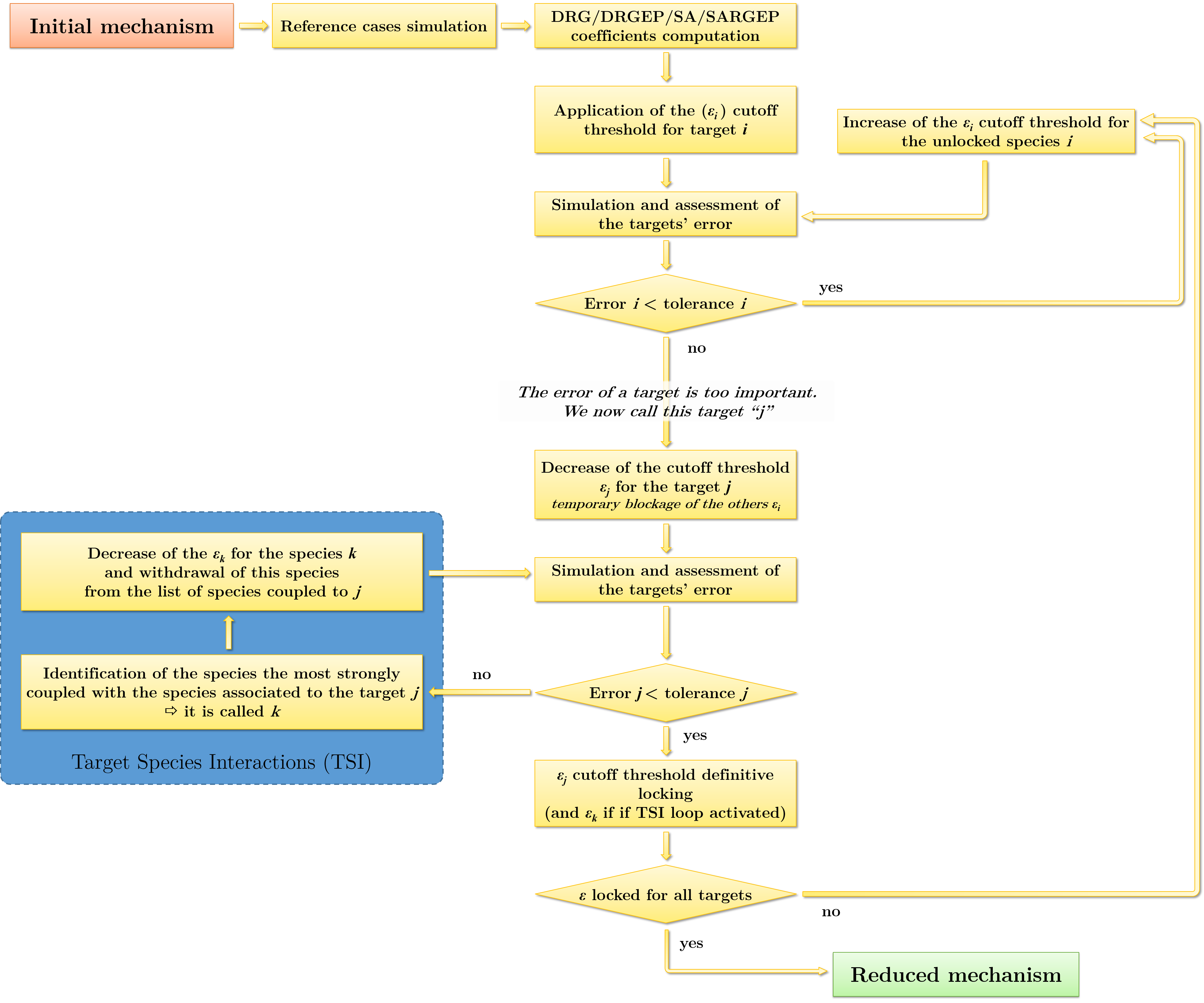
The reduction algorithm is presented in figure 2. Its structure is such that the cut-off thresholds ϵ_i for each variable of interest adapt to the error tolerance defined by the operator. These variables are independent of each other. During the reduction process they can, depending on the case, increase (for a higher species reduction), be blocked, or be decreased (for a lower species reduction).

The code has been developed in such a way that the information on the reactivity of the mixture collected by the reduction algorithms can be used to guide the optimization method. The idea is to identify the most important reactions for the simulation and to target these ones for the optimization step in order to get a better efficiency.

Examples of results

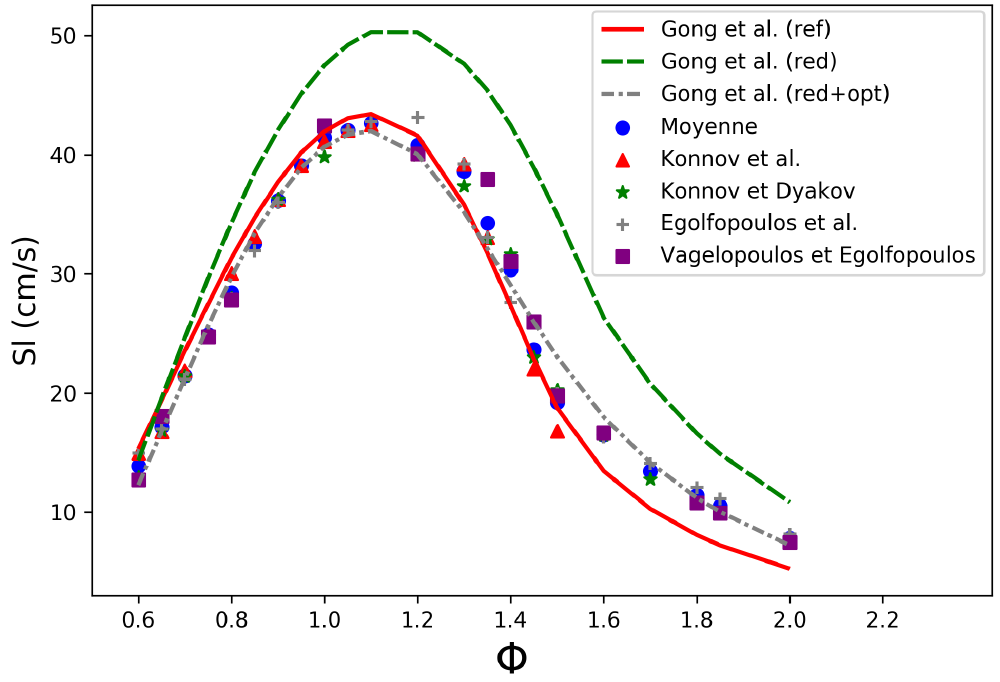
As an illustration, a reduction procedure was performed on the mechanism of Gong et al. (2015) (260 species, 1725 reactions) by using a DRG method and defining an error tolerance of up to 60\% relative to the results obtained with the original mechanism. A reduced mechanism containing 27 species and 34 elementary reactions was thus obtained and then optimized using the genetic algorithm. This optimization procedure was based on the experimental results presented in figure 3. To this end, the kinetic constants A, n , and Ea were varied over a range of +/- 15%, 3%, and 3%, respectively. As n and Ea are power terms, their range of variation has been reduced so as not to affect the rate constants too much.

After the complete procedure, the simulations performed with the reduced mechanism faithfully reproduce the targeted experimental data for all the defined conditions.