Le développement des nouvelles chambres de combustion implique un recours toujours plus massif à la simulation numérique. La simulation de la combustion doit permettre une estimation précise de taux de dégagement de chaleur, de délais d’auto-inflammation ou encore de la formation des polluants. L’emploi de modèles cinétiques réalistes est indispensable à la prédiction de ces données. Des modèles cinétiques détaillés ont été développés de sorte à fournir des estimations précises sur des domaines de pression, de température et de concentration étendus. Selon la complexité du combustible initial, le modèle détaillé peut être composé d’une dizaine d’espèces (H2) à quelques milliers (C10H22). Cependant, la résolution numérique de systèmes complexes réactifs impliquant des mécanismes cinétiques détaillés est très coûteuse en temps de calcul. Dans ce contexte, un grand nombre de méthodes numériques ont vu le jour dans le but de simplifier les modèles cinétiques, en limitant le nombre d’espèces impliquées (qui gouverne directement le nombre d’équations de conservation d’espèces à résoudre) et/ou en limitant la raideur des équations différentielles à résoudre.
Développement d’un outil de réduction de modèles cinétiques
Un outil de réduction et d’optimisation de mécanismes cinétique a été développé au laboratoire afin de les adapter pour la simulation des écoulements réactifs dans les chambres de combustion en configurations complexes. Cet outil s’appuie sur des algorithmes de réduction recensés dans la littérature (Analyse de sensibilité (SA), Directed Relation Graph (*), Directed Relation Graph with Error Propagation (**), analyse de sensibilité coupée à un graphique de relation avec propagation d'erreur (SARGEP)) puis applique, au besoin, l’algorithme génétique (***) ou l'optimisation par essaim particulaire pour optimiser les constantes de réactions du mécanisme réduit de sorte à compenser les erreurs issues de la perte d’information inhérente à la procédure de réduction.
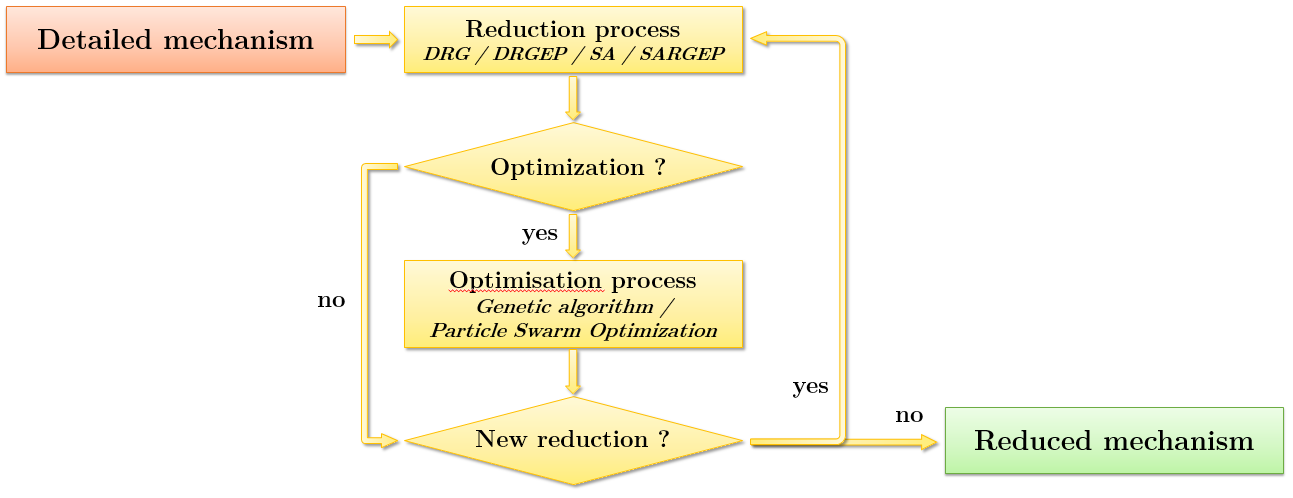
L’algorithme global du code est présenté sur la figure 1. Plusieurs méthodes de réduction peuvent être employées successivement avec ou sans optimisation.
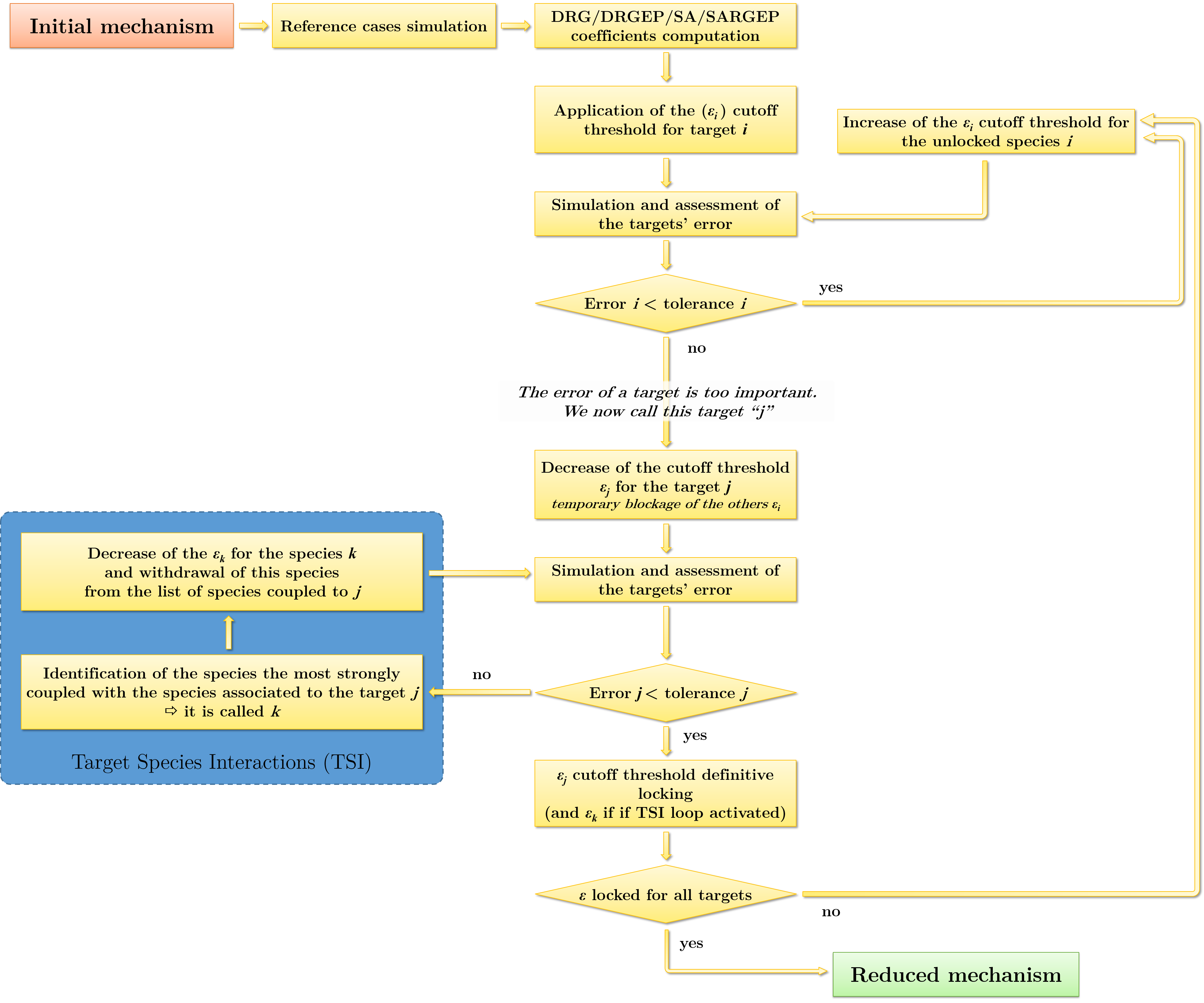
L’algorithme de réduction est présenté sur la figure 2. Sa structure est telle que les seuils de coupure ϵi propres à chaque variable d’intéret s’adaptent à l’erreur calculée. Ces variables sont indépendantes les unes des autres. Au cours de la procédure de réduction elles peuvent, selon les cas, augmenter (réduction d’espèce plus intense), être bloquées ou bien être diminuées (réduction d’espèces moins intense). A l’issue de la procédure, les résultats de simulations effectuées avec mécanisme réduit présentent, par rapport au mécanisme complet, des erreurs inférieures au seuil de tolérance préalablement défini.
Le code a été développé de sorte a offrir une grande souplesse dans son utilisation. Ainsi, les informations sur la réactivité du mélange collectées par les algorithmes de réduction peuvent être exploitées pour orienter la méthode d’optimisation. L’idée étant d’identifier les réactions les plus importantes et de cibler ces dernières pour la phase d’optimisation de sorte à être plus efficace.
Exemple de résultat
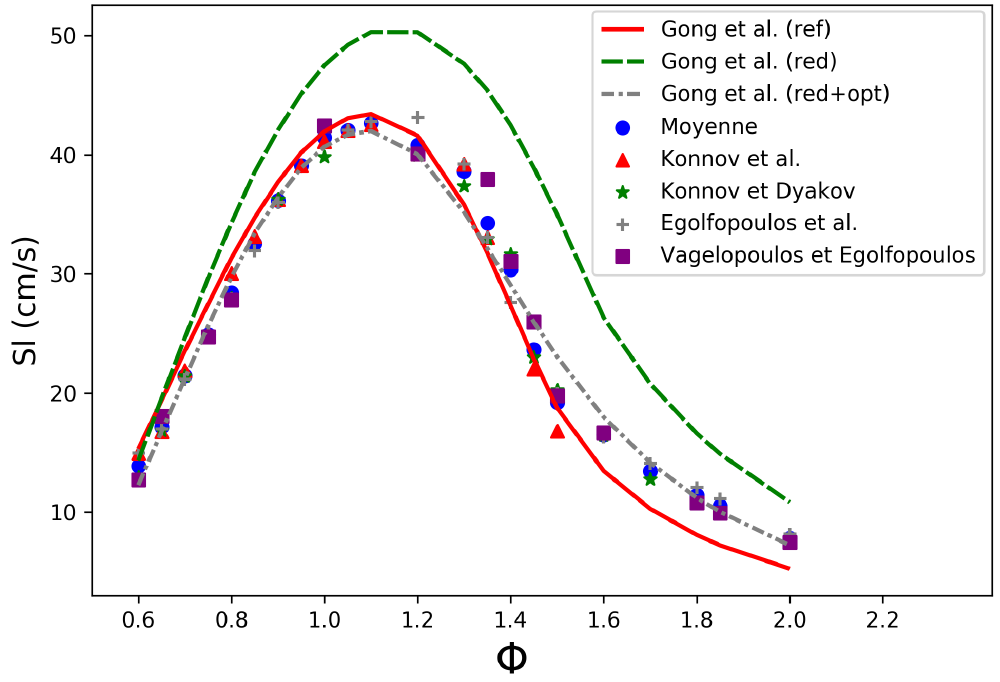
A titre d’exemple, une procédure de réduction a été opérée sur le mécanisme de Gong et al. (2015) (260 espèces, 1725 réactions) au moyen d’une méthode DRG et en définissant une tolérance d’erreur jusqu’à 60% par rapport aux résultats obtenus avec le mécanisme initial. Un mécanisme réduit contenant 27 espèces et 34 réactions élémentaires a ainsi été obtenu puis a été optimisé par l’algorithme génétique. Cette procédure d’optimisation a été effectuée par rapport aux résultats expérimentaux présentés sur la figure 3. Pour cela, les constantes de vitesse A, n et Ea ont été modifiées sur une plage de +/- 15%, 3% et 3%, respectivement. Les facteurs n et Ea étant des termes de puissance, leur plage de variation a été réduite de sorte à ne pas trop affecter la constante de vitesse.
On note en particulier qu’à l’issu de la procédure complète, les simulations effectuées à l’aide du mécanisme réduit permettent de reproduire fidèlement les données expérimentales ciblées sur l’ensemble des conditions définies.
(*) T. Lu and C.K. Law. A directed relation graph method for mechanism reduction. Proceedings of the Combustion Institute, 30(1):1333–1341, January 2005.
(**) P. Pepiot-Desjardins and H. Pitsch. An efficient error-propagation-based reduction method for large chemical kinetic mechanisms. Combustion and Flame, 154(1–2):67–81, July 2008.
(***) J.H. Holland. Genetic Algorithms. Scientific American, 267(1):66–73, 1992.
F. N. Egolfopoulos, D. X. Du, and C. K. Law. A study on ethanol oxidation kinetics in laminar premixed flames, flow reactors, and shock tubes. Symposium (International) on Combustion, 24(1):833–841, January 1992.
G. Jomaas, X. L. Zheng, D. L. Zhu, and C. K. Law. Experimental determination of counterflow ignition temperatures and laminar flame speeds of C2–C3 hydrocarbons at atmospheric and elevated pressures. Proceedings of the Combustion Institute, 30(1):193–200, January 2005.
A.A. Konnov and I.V. Dyakov. Experimental Study of Adiabatic Cellular Premixed Flames of Methane (ethane, Propane) + Oxygen + Carbon Dioxide Mixtures. Combustion Science and Technology, 179(4):747–765, March 2007.
A.A. Konnov, I.V. Dyakov, and J. De Ruyck. Measurement of adiabatic burning velocity in ethane–oxygen–nitrogen and in ethane–oxygen–argon mixtures. Experimental Thermal and Fluid Science, 27(4):379–384, April 2003.
C.M. Vagelopoulos and F.N. Egolfopoulos. Direct experimental determination of laminar flame speeds. Symposium (International) on Combustion, 27(1):513–519, January 1998.
Publications associées
E. El Rassy, A. Delaroque, P. Sambou, H.K. Chakravarty and A.M. Matynia. On the Potential of the Particle Swarm Algorithm for the Optimization of Detailed Kinetic Mechanisms. Comparison with the Genetic Algorithm. The Journal of Physical Chemistry A, 125(23):5180–5189, 2021.